Factor de potencia II
Anteriormente ya hablamos del factor de potencia .
En instalaciones con motores nos aparece un consumo derivado de la creación de campos magnéticos, lo que se entiende por inducción, esta energía es la llamada reactiva, a diferencia de la activa, no se transforma en trabajo, sólo ocasiona problemas a la red y sus componentes, nos obliga a un sobredimensionado de la instalación.
Energía aparente es la que nos suministra la compañía distribuidora.
Energía aparente es la suma vectorial de la activa y la reactiva, estas llevan un desfase de 90 grados.
La energía activa es la realiza el trabajo y también la disipada en calor. se mide en W
La energía reactiva viene de la creación de los campo magnéticos, se mide en Var
La energía aparente que es la suma de estas dos se mide en Wa
Como podemos entender la intensidad aparente es mayor cuando mayor sea la reactiva en relación a un mismo trabajo.
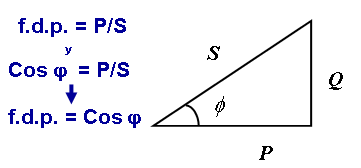
En la relación entre la energía activa (P) y la aparente (S) nos aparece el factor de potencia, llamado coseno de fi , siendo fi el ángulo que formas estos dos vectores, por otro lado al ir desfasada la reactiva 90 grados, se nos da un triángulo rectángulo donde podríamos aplicar Pitagoras
El coseno de φ es el cociente de la potencia activa P en watios y la aparente S en Va suministrada para esta potencia activa
Puede adquirir un valor entre cero y uno , cuando mas cercano este a 1 mejor sera, pues esto nos indica que la potencia absorbida se transforma en trabajo, menos las perdidas por calor. De esta manera se optimiza el consumo y se conserva la instalación.
El coseno de φ no tiene en cuenta la potencia propia de los armónicos.
La potencia en un sistema trifásico viene representada por la siguiente formula :
P = V · I · 1.73· cos φ
P- WATIOS
V- VOLTIOS
Si despejamos la I I = P / V·1.73· cos φ
de esta formula podemos ver que la intensidad es indirectamente proporcional al cos φ, cuanto mayor sea este menor sera la intensidad para una misma potencia.
Tenemos que tratar el factor de potencia hasta conseguir un valor próximo a la unidad , como lectura rápida si comparamos un cos φ igual a uno, y un cos φ de 0.50 para un mismo trabajo este último necesitaría el doble de la intensidad.
Si bien no es frecuente encontrar valores tan bajos, sí es corriente valores de 0.80, que corrigiendolos a valores de 0.99 suponen un alivio, tanto para las facturas energéticas como para los componentes de las instalaciones.
Los interruptores automáticos de control de potencia se ven afectados por la falta de corrección del cos φ, si además de añaden otros problemas de calidad del consumo eléctrico como la generación armónicos y demás perturbaciones, la instalación se aparece a un rompecabezas.

No hay comentarios:
Publicar un comentario